“The human brain, then, is the most complicated organization of matter that we know.”
Isaac Asimov

If someone asks what you recall when you look at the following pictures, I can hear you say ‘President Obama’ and ‘Statue of Liberty’. You just see a fragment of the pictures and remember them.

So, how does it happen? This is just a simple task for the brain. It stores an image and retrieves it whenever a part of it is seen. Amazing features of the brain, especially its power to learn and make decisions, inspires computer scientists in the field of artificial intelligence.

In computer science, an artificial neuron is a simple computational model of a neuron in the brain that excludes biological properties. Artificial neural networks (ANNs) are composed of artificial neurons, and they are utilized to solve specific problems, especially those that require learning and decision-making. ANNs may not be the best solutions in various machine learning problems; however, they are accepted as strong alternatives. Although ANNs don’t claim to be so, currently they are not even close to producing a simple model of the brain. Let’s take a short journey into the world of ANNs to experience the extreme difficulty of modeling the brain.

Some Applications of ANNs

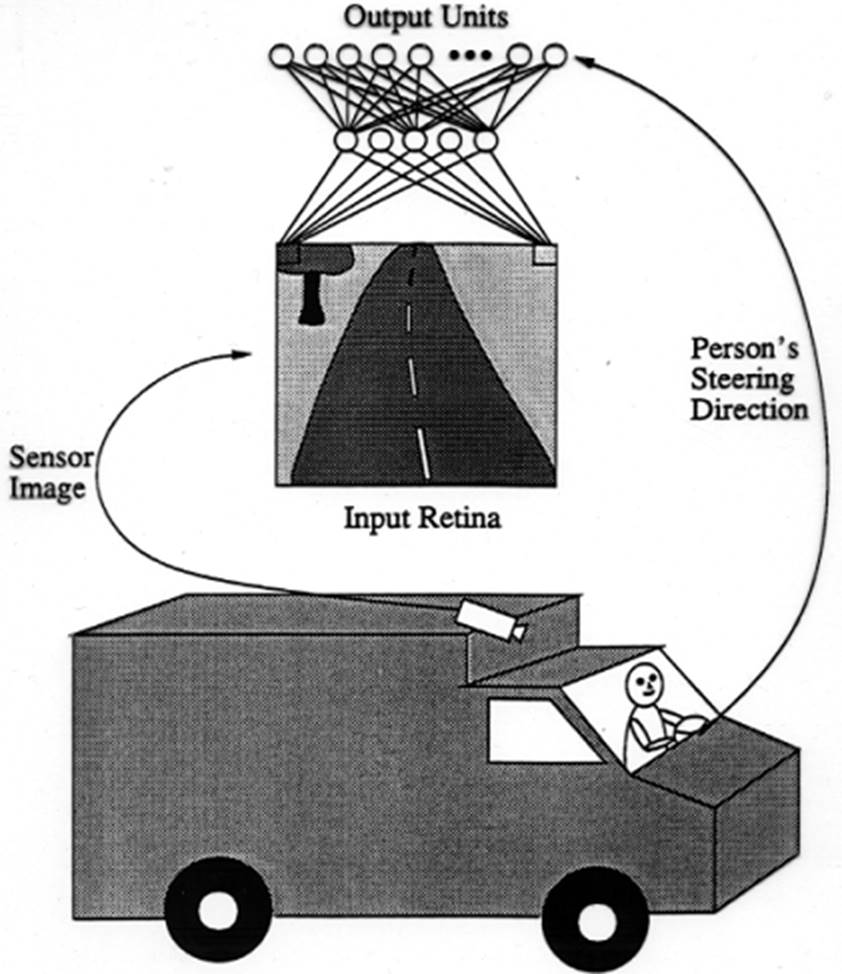
Figure 1: Overview of ALVINN structure. Images obtained from the camera installed on the vehicle are provided to the ANN, and ANN decides the steering angle.

(adapted from: http://virtuallab.kar.fei.stuba.sk/robowiki/images/e/e8/Lecture_ALVINN.pdf).

ANNs have various applications in very large spectrum of problems that require learning, such as the Autonomous Land Vehicle in a Neural Network (ALVINN). The structure of ALVINN is shown in Figure 1. The ALVINN project by Carnegie Mellon University started in 1986 and aims to make a vehicle without a driver (Mitchell, 1997). In this project, ANN learns the steering habits of a driver. A camera is mounted on the vehicle to capture the images of the road. With respect to the continuous images provided, ALVINN determines the steering level with 45 different angle positions from sharp left to sharp right. Steering is updated 15 times per second so that it allows real-time control while driving at 55 mph. The system is trained by the data obtained from a human driver in a simulator and a real vehicle. ALVINN was able to speed up to 70 mph and successfully drive at 55 mph for 90 miles.

Figure 2: Handwritten zip codes (LeCun, et al., 1989)

Another example is handwritten zip code recognition (LeCun, et al., 1989). Zip codes from US Mail written by various people with large variety of styles and sizes were used in the experiments. Figure 2 presents some examples of zip codes in the experiment database. After the ANN was trained with more than 7,000 digits in the zip codes, it was 99% successful in recognizing around 2,000 digits in new zip codes.

Learning and Decision-making in ANNs

In order to understand the challenges better, we will first examine learning and decision-making in neurons and ANNs on simple examples.

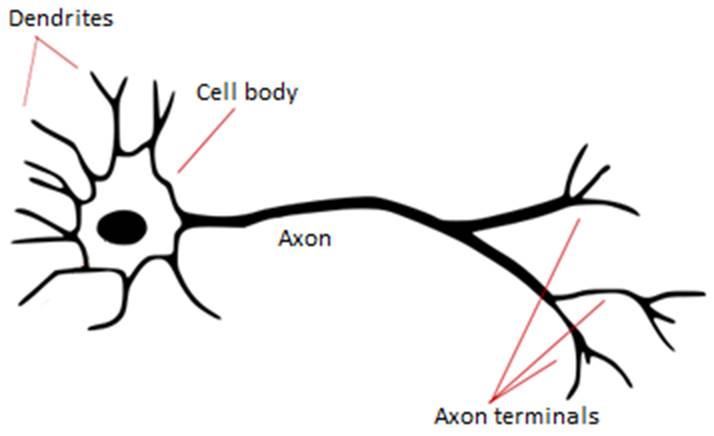
Figure 3: (a) A typical neuron (adopted from http://commons.wikimedia.org/wiki/File:Neuron_-_annotated.svg), (b) artificial neuron in computer

Figure 3(a) illustrates a typical neuron which is the constituent of brain’s complicated network structure. Each neuron receives information as signals via dendrites, then evaluates it and generates a signal that is transmitted through its axon. A neuron has many connections between its dendrites and the axons of various other neurons. Figure (b) demonstrates an artificial neuron in computer science. It is considered a function: dendrites as the inputs of the function and generated signal via the axon as the output of the function.

Let’s see an example of an artificial neuron that understands if a given produce is a red apple or not. Think about how you understand whether a produce is a red apple or not. You see the shape and the color. However, it might be an artificial one for decoration. Then you can taste it and you get the sweetness of the apple. Similarly, our neuron receives three pieces of information as the input; ‘has circular shape?’, ‘is sweet?’, and ‘has red color?’. If the output is ‘yes’, that means the neuron recognizes the produce as a red apple. Otherwise, it will be ‘no’, which means the produce is not a red apple (Figure 4). Here, the neuron’s function is defined in such a way that it only generates ‘yes’ when all the inputs are ‘yes’.

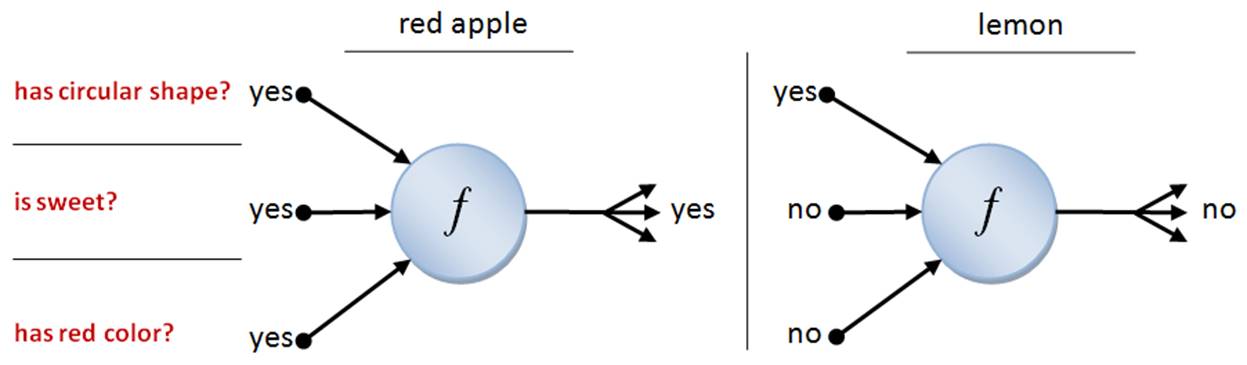
Figure 4: Example inputs and outputs for the artificial neuron.

In an artificial neuron, some of the information can be more important than the others. For instance, to have red color may be more valuable in determining the price of produce. Assume that round shape and sweetness has equal value of $1; however, having red color is $2 – twice as valuable as the other features (Figure 5).

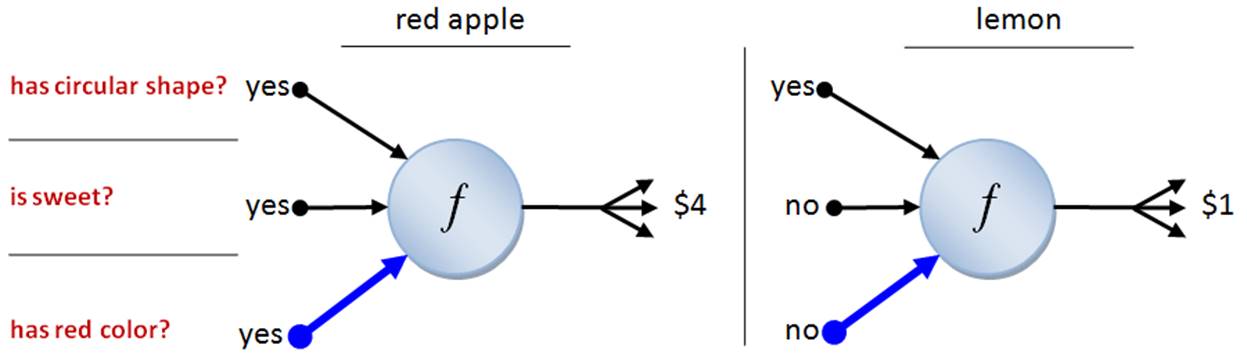
Figure 5: Artificial neuron with different input weights. Arrow thickness indicates the importance.

So, what is the big fuss about artificial neurons if they are only functions? In fact, the main feature of artificial neurons is learning. Considering the last example above, the neuron initially does not know the importance of the dendrites, i.e. the weights of inputs are all the same. If not trained, the neuron will generate the following answers which are sometimes wrong as indicated in Table 1.

Table 1: Artificial neuron before training; highlighted answers are wrong.

In real life, a teacher trains students. For instance, the teacher asks a question and if the received answer is not correct, she provides the right answer. Students learn the right answer and use this correct information in their lives. It is similar in artificial neurons as depicted in Figure 6. When the response of the neuron is incorrect, it adjusts the importance of the dendrites with respect to the correct answer hence it answers the same question correctly next time. During the training session, the neurons will be continuously asked the values of all the produce until it learns them all.

Figure 6: The learning process of the artificial neuron.

What if the problem gets complicated? Then one artificial neuron will not be sufficient, and we will need a network of neurons; ANNs. A more complex problem, ‘learning the digits’ is indicated in Figure 7.

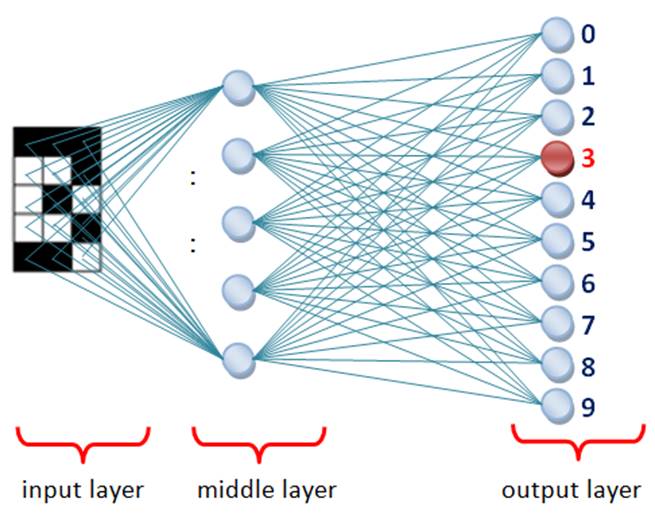
Figure 7: (a) Digit learning problem, (b) ANN structure that learns digits. Due to the difficulty, only the connections between the input layer and first / last neurons in the middle layer are shown.

ANN has 3 x 5 = 15 input units like receptors of an eye retina. Each input unit corresponds to one square in the digits; either filled or blank. Each input unit is connected to the dendrites of all neurons in the middle layer. The output of each cell in the middle is connected to the dendrites of all neurons in the output layer. There are 10 output neurons corresponding to the digits from 0 to 9. After the ANN is trained, it provides a correct answer to the given digit as input. When digit ‘3’ is provided to the network, the neuron labeled with number ‘3’ in Figure 7(b) is triggered and outputs ‘yes’ whereas the rest of the neurons output ‘no’.

Figure 8: Faulty digit '3' with a missing black square on the top right side.

Initially, all neurons in the network have equally weighted dendrites. After a reasonable amount of training, neurons adjust their weights, and ANN is able to identify digits. Here, we have some major challenges: what does ‘reasonable amount of training’ mean? When the ANN is undertrained, it will not always answer correctly to the digits given in Figure (a). In the other case, when the ANN is overtrained, it will memorize the digits provided during the training and will not recognize the faulty ones such as the one in Figure 8.

Challenges of ANNs

Beyond the mentioned the overtraining / undertraining problems, ANNs have a bigger challenge – how to determine the structure of ANN that fits the problem? In the digit learning example, we’re lucky because the structure is provided in Figure 7(b). However, the outcome of the solution may drastically depend on the number of neurons and the connections among them which is indeed a hard problem for ANNs.

The huge capability of the brain in learning and decision making comes from the huge number of neurons – around 100 billion – and the enormous amount of connections among them – from 100 to 500 trillion. The challenge to design such a huge network requires huge computation power. With the increasing number of neurons, ANN dramatically slows down especially during the learning process. Here, our example is a simple learning task of 3x5 pixel digits compared to the brain’s acquisition capacity of hundreds of images in our daily life. 

When the number of neurons gets larger, the reliability of network also reduces. Small adjustments in weights may change the entire behavior of the network hence it is easy to lose control of ANN. In contrast, the brain has a robust system, and its fault tolerance is admirable. Although neurons die every day, this doesn’t affect its performance significantly. The training method and how to update the weights are other hard problems leading to many different approaches in the neural computation field.

We have presented some simple tasks that can be solved using a few neurons and their challenges. On the other hand, consider the thousands of problems, various and incredible amount of information we have learned, and the thousands of decisions we make. The brain is truly amazing from the computer science perspective.

Bibliography

• Hertz, J. A., Krogh, A. S., & Palmer, R. G. (1991). Introduction To The Theory Of Neural Computation. Reading, MA: Addison-Wesley.
• Hopfield, J. J. (1982). Neural networks and physical systems with emergent collective computational properties. Proceedings of the National Academy of Sciences of the USA , 79, 2554-2588.
• LeCun, Y., Boser, B., Denker, J. S., Henderson, D., Howard, R. E., Hubbard, W., et al. (1989). Backpropagation applied to handwritten zip code recognition. 1 (4), 541-551.
• Mitchell, T. M. (1997). Machine Learning. McGraw-Hill.